The solution to exercise 4.1 seems to be wrong. For reference, here is the code in question:
th1 = msg.position[0]
th1 = math.atan2(math.sin(th1), math.cos(th1))
th2 = msg.position[1]
th2 = math.atan2(math.sin(th2), math.cos(th2))
dth1 = msg.velocity[0]
dth2 = msg.velocity[1]
tau_1 = -(37.587 * dth1 + 9.121 * dth2 + 13.033 * th1 + 3.718 * th2)
tau_2 = -( 7.396 * dth1 + 8.636 * dth2 + 3.114 * th1 + 1.760 * th2)
The solution code essentially solves for u with u = -Kx, where the result of the matrix multiplication is hard-coded. This is fine, except that based on the solution code, the state vector x is assumed to have the format:
[dth1 dth2 th1 th2]
However, in the first code snippet of section 4.3, we see the following two lines of code:
x0 = zeros(4)
x0[:2] = deg2rad(2.0)
The code explanation reads:
“Now we can integrate the equations of motion again, but this time with the controller in place. in order to show the effectiveness of the controller, we add a small disturbance of 2 degrees to θ1 and θ2.” In conjunction with the snippet of code above, this suggests that the first two elements of the state vector are θ1 and θ2, respectively.
So it would seem that the true format of the state vector should be something like:
[th1 th2 dth1 dth2]
To test this, I copy/pasted the solution code exactly and changed only one line:
set_joints(‘rrbot’, ‘robot_description’, [‘joint1’, ‘joint2’], [math.radians(0), math.radians(0)])
became
set_joints(‘rrbot’, ‘robot_description’, [‘joint1’, ‘joint2’], [math.radians(10), math.radians(10)])
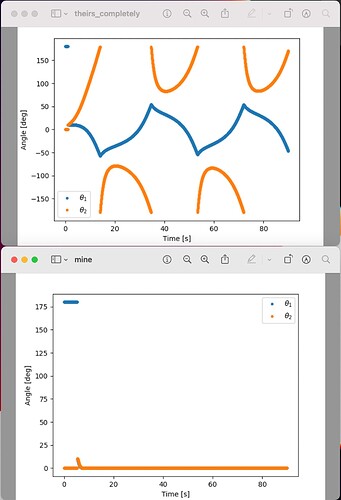
I did this just to give each controller a real test–setting the arm to an initial position different from the desired position, and seeing if it could correct itself. To be generous, I gave the controllers 90 seconds, rather than 30. Sure enough, the solution code could not properly compensate, since the state vector was out of order.
The plot on the top is the provided solution; the plot on the bottom is my own solution, which assumes the state vector has the order: [th1 th2 dth1 dth2]. I tested both controllers in the same way, initially setting both joints to 10 degrees.
Am I missing something?
If you’re looking for a quick fix, here is a copy/paste-able snippet to fix the provided code:
tau_1 = -(37.587 * th1 + 9.121 * th2 + 13.033 * dth1 + 3.718 * dth2)
tau_2 = -( 7.396 * th1 + 8.636 * th2 + 3.114 * dth1 + 1.760 * dth2)
However, I suggest also revising the evaluation code to use a different initial configuration, or otherwise somehow perturb the arm, as simply checking if it can maintain its current position (in a configuration which doesn’t even require the joints to oppose gravity) is not a good test of the controller.